쿨백-라이블러 발산은 머신러닝이든 딥러닝이든 공부를 지속해가다보면 심심치 않게 만나볼 수 있는 개념이다. 공부를 할 때마다 위키피디아를 들락날락하지 않도록 블로그에 정리해보고자 한다.
Kullback-Leibler Divergence (KLD)
KLD는 knowledge distillation, variational inference 등 두 개의 분포 간의 차이를 계산할 때 사용되는 measure이다.
정의
- X가 이산확률변수일 경우
$$D_{KL}(P||Q) = {\sum_{i} P(i)\ log\frac{P(i)}{Q(i)}}$$ - X가 연속확률변수일 경우
$$D_{KL}(P||Q) = {\int_{x} p(x)\ log\frac{p(x)}{q(x)}} $$
의미
위의 정의를 풀이하자면, 어떠한 확률분포 P가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q를 P 대신 사용할 경우의 엔트로피(정보량) 변화이다.
따라서, 원래의 분포가 갖는 엔트로피 H(P)와 P 대신 Q를 사용할 때의 교차엔트로피 H(P,Q)의 차이를 구하면,
$$D_{KL}(P||Q) = H(P,Q) - H(P) = -\sum_{i}{p(i)\ log\ q(i)} - (-\sum_{i}{p(i)\ log\ p(i)})$$
와 같다. 위의 식을 정리한다면 앞서 밝힌 KLD의 정의가 유도된다.
위의 KLD 정의는 expectation의 관점에서 해석하면, $x$가 확률분포 $p$를 따를 때 함수 $log\frac{p(x)}{q(x)}$의 기댓값을 의미한다. ($E_{x\sim\ p}[log\frac{p(x)}{q(x)}]$)
유의사항
KLD의 경우에는 대칭이 아니므로, $P$와 $Q$의 위치가 서로 바뀌면 다른 값을 갖는다는 점을 유의한다.
쓰임
다양한 쓰임이 있으나 몇 가지만 정리해본다.(추가 사항이 있을 경우 댓글로 알려주시면 조사 후 정리해넣겠습니다)
- Teacher-student network structure (knowledge distillation)
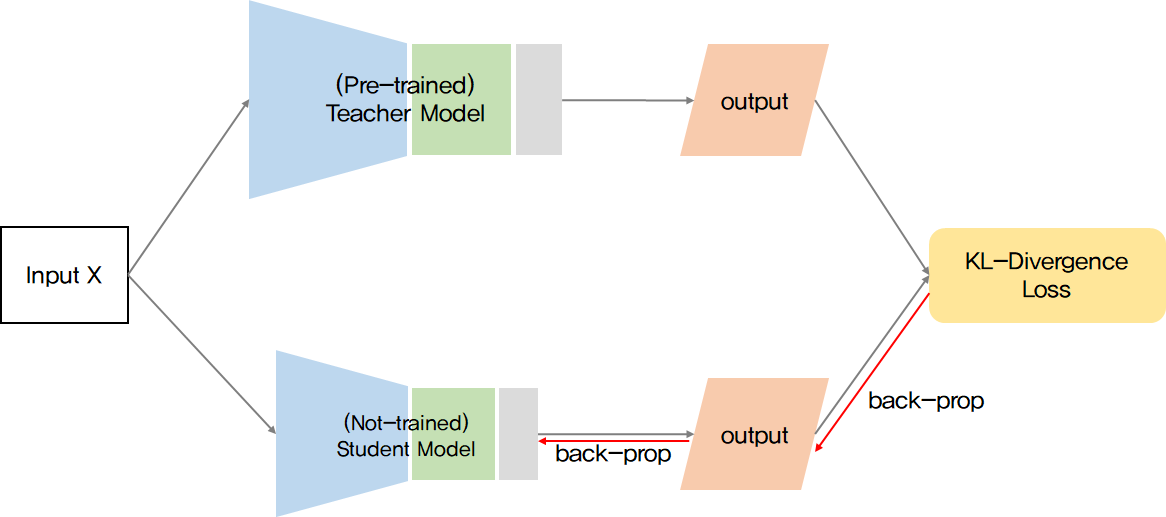
knowledge distillation은 간단히 말한다면 한 모델(teacher)이 학습한 것을 다른, 보다 작은 모델(student)에 넘겨주는 것을 의미한다. student 모델의 분포가 teacher 모델의 분포를 점차 닮아가는 형태로 학습을 진행시키면서 기존 teacher 모델의 지식을 student 모델에 주입하는 형태로 학습이 된다. knowledge distillation에서도 unsupervised learning과 supervised learning 방식으로 나뉘는데 라벨값이 없는 unsupervised learning의 경우에 사용되는 loss function이 KL-Divergence이다. 앞서 말한 teacher, student 두 모델이 점차 닮아간다는 것은 두 모델이 갖는 분포의 차이가 점차 줄어든다는 것을 의미한다. teacher를 student가 mimicking(모방)한다는 점에서 KLD의 의미와 부합함을 알 수 있다.
- Variational Inference (변분추론)
Bayes Inference (베이지안 추론)의 근간은 사후분포(posterior distribution)이다. 하지만, 사후분포를 직접적으로 구하는 것은 대부분의 경우 매우 어렵기 때문에 사후분포 $p(z|x)$를 근사하는 variational distribution $q(z)$를 구하는 경우가 많다. 이를 variational inference, 즉 변분추론이라 하며 $p(z|x)$와 $q(z)$ 간의 KLD를 구하여 근사하도록 한다. 이러한 변분추론의 개념은 생성모델인 VAE의 기본 개념이 된다.
Jensen-Shannon Divergence
앞서 말했던 바와 같이 KLD는 symmetric하지 않다는 특징이 있다. 즉, $D_{KL}(P||Q) \neq D_{KL}(Q||P)$ 이기 때문에 distance의 개념으로는 사용할 수 없다. 이를 보완하기 위해 symmetric하게 만들어준 것이 Jensen-Shannon Divergence (이하, JSD) 이다. JSD의 정의는 다음과 같다.
$$JSD(P||Q) = \frac{1}{2}D(P||M) + \frac{1}{2}D(Q||M)$$ where $M=\frac{1}{2}(P+Q)$
위읭 정의에 따라 $JSD(P||Q) = JSD(Q||P)$ 이므로, 두 확률분포 간의 거리로 활용할 수 있다.
'DeepLearning > Basic' 카테고리의 다른 글
| [Paper Review] Very Deep Convolutional Networks for Large-Scale Image Recognition (VGGNet) (0) | 2022.05.01 |
|---|---|
| [Generative Models] Generative Adversarial Networks (2014) (2) | 2022.04.05 |
| [ML/DL] 딥러닝에서의 Cascade (0) | 2021.12.12 |
| [DL] ResNet의 Inspiration (4) | 2021.09.24 |
| [ML/DL] 최적화(Optimization), 경사하강법 (Gradient Descent Methods) (2) (0) | 2021.08.21 |