convolutional layer의 output size 공식에 대한 제 나름의 이해를 간단하게 정리한 글입니다.
The output size of a Convolutional layer
[가정]
- 2-D discrete convolutions (커널 사이즈 2-D)
- input이 정사각형 (h == w)
- kernel이 정사각형
- stride의 경우 각 축에 동일하게 적용됨
- zero padding의 경우 각 축에 동일하게 적용됨
- dilation은 적용하지 않음.
[공식]
$$o = \lfloor \frac{i+2p-k}{s} \rfloor + 1 $$
- $i$ = a size of input
- $p$ = amount of padding
- $k$ = kernel size
- $s$ = stride
- $o$ = output size
convolution output size는 kernel이 i 내에서 얼마나 스텝을 밟을 수 있는지로 결정됩니다. 예를 들어, 5x5 입력에서 k=2, s=2, p=0라고 가정해봅시다.
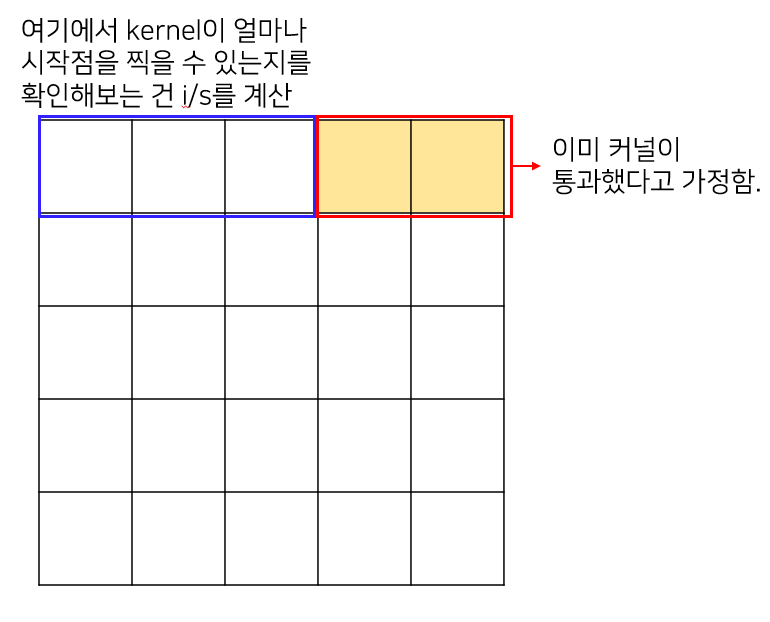
i에서 k를 미리 빼줌으로써 한 번은 이미 커널이 step을 밟았다고 해봅시다. 그렇게 되면 i-k만큼 kernel이 step을 밟을 공간이 남아있습니다 (일차원이라고 가정하면). stride가 1이라면 i-k만큼 kernel이 다 step(시작점)을 밟을 수 있겠지만, stride가 1보다 크다면 i-k를 s로 나눈 만큼만 step을 밟을 수 있을 것입니다. (징검다리를 건넌다고 생각해보면 쉽습니다. 내가 건널 수 있는 돌 개수가 n개라고 하고 k 개마다만 밟을 수 있다고 한다면 n/k개만 최종적으로 밟게될 것입니다.)

그렇다면 왜 이미 k를 빼줌으로써 이미 한 번 커널이 step을 밟았다고 해주는 걸까요? 이러한 가정이 없다면 kernel이 움직일 수 있는 공간은 (i-k+1)입니다. 이렇게 될 경우, i-k+1 = 3(이번에는 k=3으로 생각해봅시다)이 되고 이를 s=2로 나누어주면, 1.5가 나오기 때문에 floor function을 적용하면 1이 됩니다. 그러나 실제로 커널은 1번째 칸, 3번째 칸을 시작점으로 총 2번 step을 밟을 수 있습니다. 이처럼 i-k+1이 s로 나눠떨어지지 않을 경우 floor 처리를 함으로써 -1이 되는 문제를 방지하기 위해 미리 하나를 제해놓는 것입니다.
따라서, $o=\lfloor \frac{i+2p-k}{s} \rfloor + 1$으로 결정이 되는 것입니다. padding 값을 더해주는 건 i의 크기가 늘어나는 것과 다를 바가 없기때문에 p가 주어지는 상황은 예시를 들지 않았습니다.
위와 같이 직관적으로 convolution 연산의 output size formula에 대해 알아보았습니다. 상기한 내용에 오류가 있다면 댓글 부탁드립니다. 약간의 궁금증은 남아있습니다만(왜 $\lceil \frac{i+2p-k+1}{s} \rceil $을 사용하면 안되는 걸까..등의?ㅎㅎ) 혹시 답변이 가능하시다면 그 부분 또한 댓글 부탁드립니다.
'DeepLearning > Basic' 카테고리의 다른 글
| [DL] Webly-supervised learning (0) | 2023.04.05 |
|---|---|
| [DL] Data Shuffling에 대한 짧은 고찰 (0) | 2022.10.19 |
| [Paper Review] Very Deep Convolutional Networks for Large-Scale Image Recognition (VGGNet) (0) | 2022.05.01 |
| [Generative Models] Generative Adversarial Networks (2014) (2) | 2022.04.05 |
| [ML/DL] 쿨백-라이블러 발산 (Kullback-Leibler Divergence) (0) | 2022.03.25 |