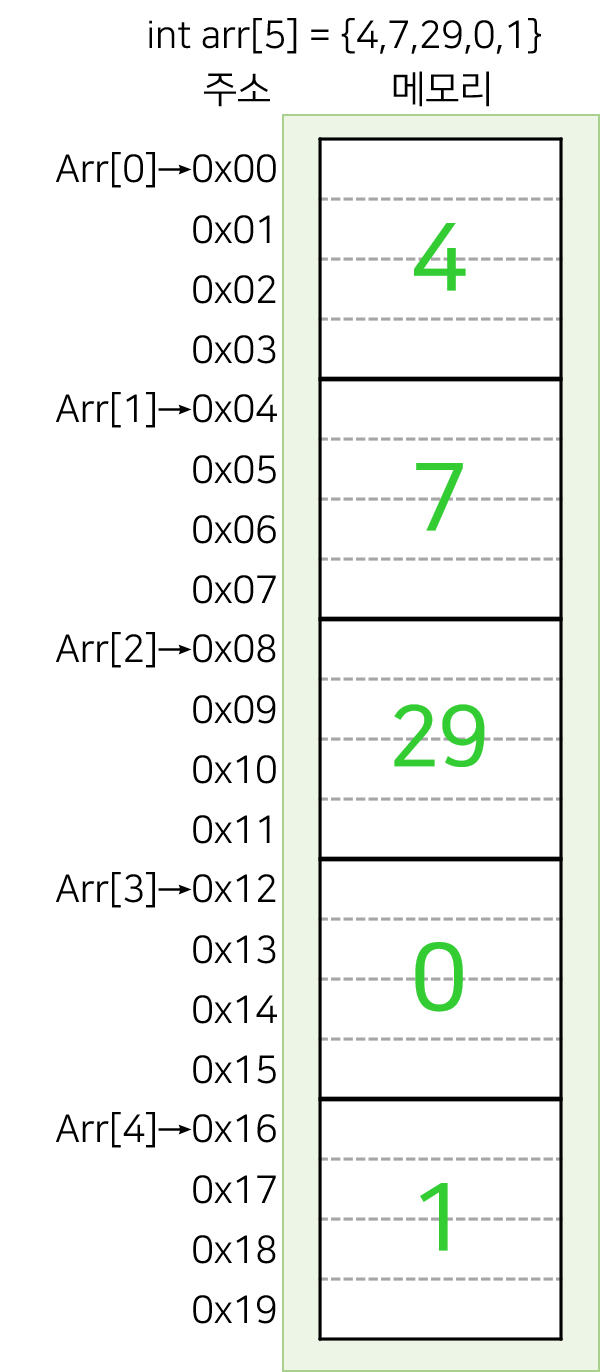
소수를 대량으로 빠르게 찾는 알고리즘이다. 소수는 1보다 큰 자연수 중 1과 자기 자신만을 약수로 갖는 수이다. 자연수 n이 소수인지 아닌지를 판별하기 위해서는 단순히 2부터 n-1까지 반복하면서 나누어 떨어지는지 확인하면 된다. 하나라도 나누어 떨어지는 수가 존재한다면 1과 자기자신을 제외한 수 중 약수를 갖게 되는 것이므로 n은 소수가 아니다. 위의 과정을 Python 코드로 표현하면, def is_prime_number(n): for i in range(2,n): # 2부터 n-1까지 if n % i == 0: # 하나라도 나누어 떨어지는 수가 있다면 return False # 소수가 아니다. return True 위의 방법은 직관적이지만 비효율적이라는 단점이 있다. 2부터 n-1까지 반복해야 하기..